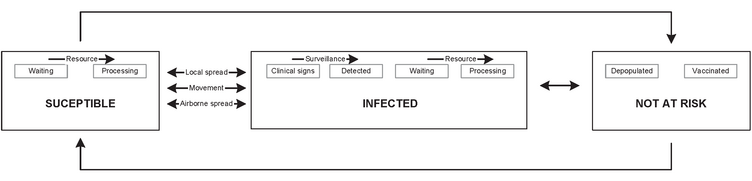
InterSpread Plus is computer program designed to provide a framework for modelling the spread of infectious disease among animal (and human) populations (Stern, 2003). The program is written in C++ (Stroustrup, 2000) and is compiled to run on either the Microsoft Windows or Linux operating systems. In the Windows version the user is able to specify model parameters via a graphic user interface. Once appropriate parameters have been defined they are passed to the C++ executable located on the same computer, or to copies of the C++ executable located on computers within a local area network. The later mode of operation is typically used when multiple models are to be run simultaneously.

A central data requirement of InterSpread Plus is explicit description of the population at risk. This consists of Cartesian coordinates defining the position in space where members of the population at risk reside. At each location the number of individuals present are specified as count data with the option to stratify these counts either by species (e.g. cattle, sheep, pigs, goats, and deer) or by type (e.g. dairy cattle, beef cattle). Location details can be specified as either discrete polygonal units or as points. To define location details in polygon format, a series of Cartesian coordinates is used to define the vertices of the boundary of each area. To define location details in point format a single set of coordinates are used: typically the position of the farm centroid. In addition to defining the number of individuals present, the model allows descriptor variables to be associated with each location. In an agricultural context these are typically used to specify farm enterprise type (e.g. 'dairy', 'beef breeding', 'beef fattening', and 'mixed'). Once defined, parameters can be associated with these descriptors, allowing their behaviour to be characterised within the model with greater control. For example regular, short distance movement patterns might be parameterised for locations with a 'dairy' descriptor whereas infrequent, longer distance movement patterns specified for those described as 'beef breeding.' The model also allows for non-farm locations to be defined which allows locations where individuals congregate on a regular or intermittent basis to be represented. This facility is typically used to represent animal markets, fairs, or rodeos. In the absence of measures to control disease these aggregation point represent an important mechanism for rapidly dispersing disease throughout the population at risk.

InterSpread Plus is a state transition model (Isham, 1993) which means that the units of interest (farm locations) exist in one of several states at any time (Figure 1). The states within InterSpread Plus include susceptible (individuals present at a location are susceptible to infection); infected (individuals present at the location have been exposed to infective agent and are either incubating disease or showing clinical signs) and; not at risk (sanitary measures have been applied to render individuals incapable of becoming infected). As sub-categories of the infected state, the model defines the states of: clinical signs (individuals on a farm are infected and showing signs of clinical disease) and detected (individuals on the farm have been identified as infected). As sub-categories of the infected and susceptible state the model defines the states of waiting (farms are queued to receive sanitary measures) and; processing (individuals on farms are receiving sanitary measures). If vaccination and pre-emptive depopulation were used as control strategies additional states under the category of not at risk might include vaccinated and depopulated. A depopulated state implies that all individuals have been removed from the location and that the location is no longer infectious; a vaccinated state implies that the location ceases to be susceptible to infection once a sufficient period of time has elapsed from the vaccination event.

Figure 1: Diagram showing the states defined within InterSpread Plus: susceptible, infected, and not at risk.

'Classical' approaches to state transition modelling consider the population at risk in terms of counts of population units present in each state at given time periods and use differential equations to regulate the transition of individuals from one state to another (Anderson and May, 1991). The key difference between this and the approach adopted by InterSpread Plus is that in InterSpread Plus population units (farm locations) are individually defined and simulation determines the transition of each unit from one state to another during each time period. While this increases the amount of computing time required to run simulations the advantage is flexibility: the behaviour of population units can be defined on the basis of class, state, location, and/or time and throughout the course of a simulation population units can be flexibly re-grouped.

To simulate an epidemic of disease it is necessary to firstly consider how a disease spreads throughout a population in the absence of control measures and secondly to consider how control measures influence the subsequent course of disease spread. In the case of FMD, virus introduced into a primary case farm infects susceptible animals on that farm and once these animals become infectious, disease is transferred to other farms by combinations of movement, local, and/or airborne spread (Henderson, 1969; Gloster et al., 1981; Gloster at al., 1982). This phase --- the unhindered spread of disease throughout the farm population --- has been termed the 'silent spread phase' of an epidemic (Anonymous, 2003). The probability that disease will be detected depends on the intensity of the 'background' level of surveillance, specified by the user. Once the presence of disease was been recognised (i.e. detected) the model allows the following activities related to control to be simulated: (1) depopulation, (2) vaccination, (3) surveillance intensity, (4) effectiveness of backward and forward tracing, (5) restriction of movements, and (6) movement standstill. All control activities are subject to user-specified resource constraints.

InterSpread Plus simulates in single time period steps, which in the case of FMD equates to periods of one day. For many steps in the simulation pathway the chance that an event occurs is defined on the basis of probability distributions that can be specified by the user. This facility introduces a stochastic element into the simulation process and for this reason a number of iterations of a model are undertaken to generate a distribution of predicted outcomes rather than a single number. In practical terms this allows decision makers to distinguish between strategies that are highly predictable (that is, strategies where the variance of the predicted outcomes is small) and strategies that are less predictable (those where the variance of predicted outcomes is large): risk averse decision makers preferring strategies that are highly predictable over those that are not.

When simulating the spread of disease on an ongoing basis during an actual epidemic, details of cases identified up to a given point in time (the epidemic history) can be used to provide the starting point for simulation. Epidemic history details are supplied to the model in the form of two data sets: (1) a state file which defines each location's state throughout the history period; and (2) an animal file specifying the number of individuals at each location at specified time periods. In the case of simulating an FMD epidemic this facility allows actual events to provide the starting point for a simulation. Inclusion of these details is important since control activities undertaken to a given point in time are highly influential in determining the subsequent epidemic course (Sanson, 1993).

Outputs from the model are presented as user-defined, space delimited ASCII text files. Three types of output are available. The first output lists, for each time period of each iteration, those locations experiencing a change of state. The second output type lists, for each time period and for each iteration, those locations in a given state. The third output type lists, for each time period for each iteration, counts of animals at each location. Thus, to list incident infections during each time period a change of state report would be requested, where the trigger state was infected. Similarly, to list depopulated farms the trigger state would be set to depopulated. Model outputs are typically passed to a statistical package or spreadsheet for analysis. Standard reports might include descriptive statistics of the predicted number of infected premises per iteration, cumulative epidemic curves, and density plots showing the number of locations predicted to become infected per unit area. A package of functions to implement these reports, written in the S language (Becker et al., 1988), is available from the model developers on request.

References

Anonymous (2003) Epidemiological Modelling Project Report - The Silent Spread Model. Risk Solutions, London.

Anderson R, May R (1991) Infectious Diseases of Humans: Dynamics and Control. Oxford University Press, Oxford.

Becker R, Chambers J, Wilks A (1988) The New S Language. Wadsworth, Pacific Grove, California.

Gloster J, Blackall R, Sellers R, Donaldson A (1981) Forecasting the airborne spread of foot-and-mouth disease virus over the sea. Veterinary Record 108, 370 - 374.

Gloster J, Sellers R, Donaldson A (1982) Long distance transport of foot-and-mouth disease virus over the sea. Veterinary Record 110, 47 - 52.

Henderson R (1969) The outbreak of foot-and-mouth disease in Worcestershire. An epidemiological study: with special reference to spread of disease by wind-carriage of virus. Journal of Hygiene 67, 21 - 33.

Isham V (1993) Stochastic models for epidemics with special reference to AIDS. Annals of Applied Probability 3, 1 - 27.

Sanson R (1993) The development of a decision support system for an animal disease emergency. Unpublished PhD thesis Massey University, Palmerston North, New Zealand.

Stern M (2003) InterSpread Plus User Guide. Institute of Veterinary, Animal, and Biomedical Sciences, Massey University, Palmerston North, New Zealand.

Stroustrup B (2000) The C++ Programming Language, 3rd edition. Addison-Wesley Professional.